Ulusal Mimarlık Öğrencileri Buluşmasının Ardından

 

7. Ulusal Mimarlık Öğrencileri Buluşması’nda Mimarlığın Doğrusal Olmayan Denklemleri başlığı altında bir araya gelen öğrenciler adına söylenecek birşeyler var ise buna bağışlanma dileğiyle başlamak gereklidir.  Bağışlanmak; çünkü biçim bulan bireysel düşünceleri (ki her biri kendi adına çok özgündüler) bir araya getirmek, son aşamada metni ele alan kişi olarak bana düştü.  Bu ifadeden bir gönülsüzlük anlamı çıkarılmasın; bunu büyük bir istek ve gönüllülükle üstlendim ama bitmişliğiyle var olan düşünceleri bir araya getirirken özgünlüklerini bozacak olduğum için tüm katılımcılardan bağışlanma diliyorum.

 

Bir diğer bağışlanma da düşüncelerin zamanında kayda alınamamasından dolayı gerekiyor. Ne yazık ki şu anda tartışma platformunda ortaya çıkan düşüncelere ancak bulanık bir filtre arkasından bakabiliyoruz.  Bu bulanıklığı, yine metni son ele alan kişi olarak, kendi yorumlarımla netleştiriyorum / bulanıklaştırıyorum.

 

Mimarlığın Doğrusal Olmayan Denklemleri temalı bir araya gelişte tartışma platformunun ortaya konuşu ve düşüncelerin biçim bulup gelişmesinde hedeflenen, “kesin” gözüyle baktığımız gerçeklerin sorgulanmasıydı.  Mimarlıkta kesin ve mutlak doğru bir tasarım olmadığını kabul edilen bir görüştür.  Buna rağmen bir çok kalıp ve kural, günümüz mimarlık praksisinde varlığını hissedilen biçimde göstermektedir.  Acaba mimarlık ve sanat öğretisinde geçerliliğine –hatta bunun da ötesinde gerçekliğine sığındığımız bu kalıp ve kurallar aynı zamanda bizi esir eden prangalar mı?   Bunu tartışmak amacıyla açılış Öklidyen Olmayan Geometri konusunda kısa bir bilgi paylaşımı ile yapıldı.  Derken kendimizi belirsizlik kuramına, Baudrillard’ın ‘Simulacra &  Simulation’una, Semiyoloji, Derrida ve Eisenman’ın düşüncelerine inen “tavşan deliğinden” aşağı yuvarlanırken bulduk.

 

Gerçekleştirilen bu tartışma ve paylaşım platformunun tortularıyla oluşan ve İlgilenenlerin http://www.muhteshambr.itgo.com/mdod.htm sayfasında yer alan metinde bulabilecekleri bir takım derlemelerle Mimari ve Gerçeklik konuları irdelenmeye çalışılmıştır.  Bu metnin tüm olumlu yönlerini, aşağıda adını andığım insanlara ve herkesten çok Gökhan Akdeniz’e borçluyum.  Özellikle Öklidyen olmayan geometri tartışılırken ve “hiperbolik yüzey geometrisi” gibi anahtar sözcüklerin yoğunlukla kullanıldığı sırada veridiği Le Corbusier’in 1958 Phillips Pavyonu örneği karşasında gözlerim büyüdü.  Mimarinin Doğrusal Olmayan Denklemleri konulu atölye çalışmasını kafamda tasarlamama neden olan Eisenman ve Jencks söyleşisinde, Jencks’in  tam da bu örneği kullanmasını nasıl açıklayacağımı hala bilmiyorum. Ayrıca Baudrillard’la ilgili bölüm, tamamen onun katkısıyla oluştu. Kendisine değerli katılımı için bir kez daha teşekkür etmek isteirm.  Okuyacağınız metindeki tüm olumsuzllukların ise sadece bana ait olduklarını yinelemek istiyorum.  

 

Selim Ökem.

 

Mimarinin Doğrusal Olmayan Denklemleri düşünsel platformu ve metninin oluşmasında aşağıda adı yazılı olan herkese ve her fırsatta benimle tartışıp teorik fizikten güncel politik konulara, yaşama ve mizha kadar düşüncelerimi şekillendiren Refik Turhan’a teşekkürlerimi sunuyorum:

 

Gökhan Akdeniz (Anadolu Üniversitesi)

Utku Uçar (DEÜ)

Nevzat Efe Çelimli (İTÜ)

Elif Nihal Kamiloğlu (KTÜ)

Elif Selcen Çetin (KTÜ)

İnci Kasap (YTÜ)

Mimarinin Doğrusal Olmayan Denklemleri

 

5. Aksiyom

 

Antik Yunan’da Öklid’in temel prensiplerini ortaya koyduğu ileri sürülen aksiyomlardan 5’incisi olarak bilinen paralellik aksiyomunun, Gauss ve çağdaşı diğer matematikçiler tarafından çürütülüşüne kadar 2000 yılı aşkın bir sürenin geçmesi gerekmiştir.   Öklid’in parallellik aksiyomu iki boyutlu bir uzayda,  bir doğru üzerinde yer almayan noktadan geçen ve bu doğruyu kesmeyen ancak tek bir doğru olduğunu öngörmektedir. 

 

Üzerinde çalışılan yüzey eğer düz bir yüzeyse bu doğrudur ancak yüzey eğrilik kazanınca işler bir hayli değişmektedir. Küresel bir yüzey üzerinde çalışılıyorsa (ki küresel yüzey üzerinde doğru, negatif sonsuzdan pozitif sonsuza dek uzatılamayacağı için tam bir doğru değildir ancak ileride görülebileceği gibi kuramsal bir başka yüzeyden bahsetmek olasıdır. Bu “başka” yüzey üzerinde doğru iki yönde sonsuza dek uzatılabileceğinden “doğru” tanımlamasını tamamen karşılamaktadır) 5. aksiyomda öngörülen verili bir doğru üzerinden geçmeyen ve o doğruyu kesmeyen bir çok doğru çizilebilir.

 

 

Aslında küresel bir yüzey düşünüldüğünde (yine 5. aksiyomla bağlantılı olarak) bir üçgenin iç açıları toplamı 180 derecedir önermesi de geçerliliğini yitirmektedir.  Küresel bir yüzey üzerinde yer alan yeterince büyük bir üçgenin iç açılarının toplamı 180 dereceden büyüktür (Aşağıdaki örnekte iç açılar toplamı 270 derece olan bir üçgen görülmekte).

 

 

Peki nasıl bir yüzey tanımlanmalıdır ki üzerinde doğru tanımını tam olarak yerine getiren bir doğru çizilebilsin (küresel bir yüzey üzerinde doğru her iki yönde de sonsuza dek uzatılamayacağını bir kez daha hatırlayalım)?  Böyle bir yüzey hiperbolik bir eğrinin kendi etrafında döndürülmesiye oluşan bir cismin yüzeyi olarak tanımlanabilir. y=1/x²  fonksiyonuyla tanımlanan ve x’in origin noktasına (sıfıra) doğru aldığı  her değer için y’nin sonsuza yaklaştığı bir eğrinin grafiğini düşünün.  Bu grafik x ve y eksenlerini sonsuza dek kesemeyecek ve bu eğrinin her hangi bir eksen etrafında döndürülerek tanımlandığı cismin yüzeyinde yer alan bir doğru her iki yönde de sonsuza dek uzatılabilecektir. Bu cisme pseudosfer (sahte küre) ismi veilir ve kuramsal bir cisimdir.  Aşağıda bu cismin bir parşasına ait model görülmektedir.

 

 

Bu cismin yüzeyinde artık tanımlarının gereğini tam olarak yerine getiren bir doğru çizilebilir ve 5. aksiyomun önermesinin aksine, bu doğru üzerinde olmayan bir nokta üzerinde yer alan ve bahsedilen doğruyu kesmeyen birden fazla doğru çizilebilir.

 

Olanaksız Operasyonlar

 

Öklidyen olmayan geometri üzerine söylenebilecek bir diğer konu da bir birine eş üçgenler ve bunların üs üste getirilebilirliğiyle ilgilidir.  Gelenksel geometride birbiriyle çakıştırılabilen (süperpoze edilebilen) her şekil birbirine eştir (if two figures can be superposed they are directly congruent).  Ancak her birbirine eş şekil, verili  iki boyutlu yüzey üzerinde kaydırılarak ya da sürüklenerek üs üste getirilemeyebilir. Bir birine eş olma kavramını biraz açalım.  Öklid eş (congruent) üçgenleri şöyle tanımlıyor:  Bir üçgenin kenar uzunlukları bir diğeriyle aynıysa bu iki üçgen bir birine ‘eş’tir.  Bir üçgen ve bu üçgenle aynı yüzey üzerinde yer alan doğruya göre bakışımı düşünüldüğünde bu iki üçgen şeklinin bir birine eş olduğu, tanımı gereği söylenebilir.  Ancak bu iki üçgeni, bulundukları yüzey üzerinden ayırmadan, üst üste getirmek (çakıştırmak= süperpoze etmek) tam olarak mümkün değildir.  Bu durumda bu iki üşgen şekil birbiriyle ‘eş’tir ancak üst üste gelmeyen şekillerdir demek gereklidir. Gerçekten de bu iki şekli bir birinin üstüne koyup tam olarak bir biriyle çakıştırmak için bakışım ekseni olan doğru üzerinde döndürmek gerekir.  Ancak  o zaman bulunduğunuz yüzey üzerinden ayrılmış ve üçüncü boyutu hesaba katmayı gerektiren geometrik bir operasyon gerşekleştirmiş olursunuz.   Bu da çalıştığınız uzayın kurallarıyla superpozisyon işleminin gerçekleştirilemeyeceği anlamınadır.  Ancak tanımlanacak başka bir iki boyutlu yüzeyle bu iki eş fakat çakışmayan şekil birbiriyle çakıştırılabilir hale getirilebilir.

 

 

Yukarıdaki resimde, kendileriyle aynı yüzey üzerinde yer alan bir doğruya göre bakışımı alınmış eş üçgen şekiller görülmektedir.  Bulundukları yüzeyden ayrılmadan, sadece bu yüzey üzerinde hareket ettrilerek bir birleri üzerine getirilemeyen bu üçgenleri çakıştırmanın (süperpoze) yolu bakışım dogrusu etrafında döndürmektir.  Ancak bu operasyon, döndürülen şeklin yüzeyden ayrılmasını gerektirmektedir.  Diğer bir deyişle, çalışılan uzayın bu işlem için yetersiz olduğu söylenebilir.  Burada belirtmek gerekir ki Öklid geometrisi bir yüzey geometrisidir ve yapılan tüm işlemler iki boyutlu bir uzayda gerçekleştirilmelidir.   Bu geometriyi eleştirecek ve önermelerini geçersiz kılacak yeni önermelerde bulunmak için yine bu iki boyutlu uzayda kalmak gerektiğini söylemek gereklidir.  Söz konusu önermeleri geçersiz kılmak için gerçekeleştirilecek tüm işlemler yüzey geometrisi işlemleri olmalıdır.

 

Möbius Bandı (belki de olanaklıdır)

1849 yılında mucidi olan August Möbius’un ismiyle anılan bir yüzeydir.  Bu yüzeyi hayal edebilmek için, bir kağıt şeridin iki ucunun bir birine, bir ucun üst kenarı diğer ucun alt kenarı ile öpüşecek biçimde kıvrıldığı düşünülebilir.  Bu şekilde elde edilen kağıt yüzeyi Möbius bandı olarak adlandırılmaktadır.  Yukarıda, birbirinin bakışımı olan ‘eş’ üçgen şekillerin, üçüncü boyutta bir operasyon gerçekleştirmeden çakıştırılamadığı gösterilmişti.  Aşağıdaki resimde Möbius’un yarattığı eğrilikli yüzeyi ve  bu iki bakışık eş üçgenin çakıştırılabileceği görülmektedir.  Açık ve koyu renklerle ifade edilen iki ‘eş’ üçgenden açık olanının Möbius şeridi üzerinde kaydırıldığında şeklin seyahati sonunda bakışığı olan diğer üçgenle çakıştığı (süperpoze olduğu) görülmektedir.

 

Öklid geometrisinin ilgilendiği şekiller Öklidyen Olmayan Geometride  farklı olmamasına rağmen işlemlerin gerçekleştiği uzayın boyutsal özelliklerini sabit tutmak koşuluyla, biçimsel özellikleriyle oynamanın yeni olanaklar ortaya koyması bir saptama olarak kaydedilmelidir ^[1]

 

Phillips Pavyonu: Öklidyen mi değil mi?

Öklidyen Olmayan Geometri’in hiperbolik parabol eğrilerin tanımladığı yüzeylerle ilgi bir geometri türü olduğu belirtilmişti.  Tasarımın biçimsel anlamda Öklidyen Olmayan Geometriyle bire bir ilişkisini kurmak olası değildir.  Buna gerek olup olmadığı da sorgulanmalıdır çünkü burada vurgulanmak istenen farklı bir durum söz konusudur.  Yine de tasarım anlamında çift eğrilikli yüzeyler ve bu yüzeylerle oluşturulmuş örtü sistemlerine göndermede bulunmak mümkündür.   Bunlardan en önemlilerinden bir tanesi  Le Corbusier’in Brüksel’de Expo ’58 için tasarladığı Phillips pavyonudur. 

 

 

 

Pavyon büyük oranda o dönemde yardımcılığını üstlenmiş olan (aynı zamanda müzik kompozitörlüğü de yapan) Iannis Xenakis tarafından tasarlanmıştır.  Le Corbusier ve Xenakis ile birlikte tasarıma katılan Edgar Varese’in bu pavyon için sentezlediği Poéme Electronique adlı müzikal kompozisyon 400 farklı hoperlörden, daha önceden kugulanmış bir sisteme göre çalındığında, kimsenin daha önceden deneyimlememiş olduğu mimari bir mekan ortaya koymuştur.  O dönem için tamamıyla devrimsel olan bu mimari form ve sesin mekan içerisinde hareketi dönemin koşulları için pahalı bir teknik gerektirmiş ve pavyon yıkıldıktan sonra bir daha tekrarlanamamıştır.  ^[2] Aşağıda Varese’in Poéme Elecronique için yaptığı çizimi  ve ilgili eserinin grafik gösterimi görülmektedir.  ^[3]

 

 

 

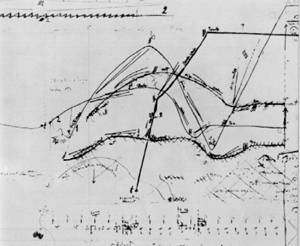
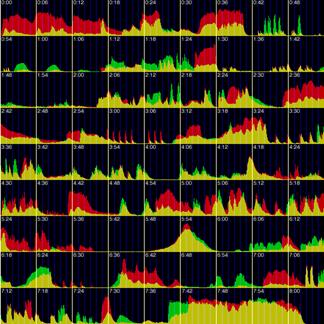
Jencks bu tasarım için şunlzarı söylüyor:

“ Le Corbusier’nin 1958’deki Philips Pavyonuyla yeni paradigma içinde sadece inşaa eden değil onu anlayan kişilerden ilki olduğunu söylerdim. (Yeni medyanın bir örneği olarak)  ışık ve ses gösterisi düzenlemişti. Biomorfik formlu, planda bir insan biçimi, cephede eğri hiberbolik parabol (böylece biyoloji ile ilişkili grameri de anlamış olduğu soylenebilir) kullanmıştı. Işık ve ses gösterisinde yeni paradigmanın anahtar unsuru olarak kozmik ikonografiyi benimsemişti. Tüm bunların hepsini bilgisayar olmadan tek bir binada kullanmıştı (yıl 1958).” ^[4]

 

Heisenberg: Tanrı Yeniden Var Oldu..

Bilimsel kuramların, özellikle  Newton'ın çekim yasasının başarısı, ondokuzuncu  yüzyılın  başında Fransız bilimcisi Marki Laplace'ı  (Laplas)  evrenin tümüyle belirlenir olduğu savına vardırdı. Leplace’ın önerdiğine göre, öyle bir bilimsel yasalar takımı olmalıydı ki, yalnızca bir an için evrenin tümünün durumunu bilirsek evrende olup bitecek her şeyi hesaplayabilirdik. Örneğin, güneşin ve gezegenlerin bir andaki hızlarını ve konumlarını biliyorsak, Güneş Sisteminin başka zamanlardaki durumunu Newton'ın yasalarını kullanaralk hesaplayabilirdik. Bu bağlamda belirlenirlik oldukça açık gözüküyor ama Laplace bununla kalmayıp insan davranışları da içinde olmak üzere her şeye hükmeden benzeri yasaların varolduğunu ileri sürdü.

 

Bilimsel belirlenirlik öğretisine, Tanrının dünya işlerine karışma özürlüğüne saldırıda bulunduğu için pek çok kişi şiddetle karşı çıktı. Yine de, bu yüzyılın başına dek bilimin olağan bir varsayımı olarak kaldı.  

 

1926'da bir Alman bilimcisi Werner Heisenberg, ünlü belirsizlik ilkesini ortaya koyunucaya dek anlaşılamadı. Bir parçacığın gelecekteki konumunu ve hızını hesaplayabilmek için şu andaki konumunun ve hızının kesin olarak ölçülebilmesi gerekir.  Bunu yapmanın en kolay yolu parçacığa ışık tutmaktır.  Işık dalgalarının bir bölümü parçacığa çarpıp saçılacaktır ve buradan payrçacığın konumu saptanacaktır.  Ancak parçacığın konumu ışığın iki dalga tepesi arasındaki uzaklıktan daha küçük bir hata ile saptanamayacağından, parçacıgın konumunu daha kesin ölçmek için daha kısa dalga boylu ışık kullanmak gerekir.  Bu tek tanecik dokunduğu parçacıgın hızını önceden bilinemeyecek bir biçimde değiştirecektir. Üstelik, konumu daha kesin ö1çebilmek için daha kısa dalga boylu ışık gerekecek ve bundan dolayı tek bir taneciğin enerjisi daha da yüksek olacaktır.  O halde parçacık daha fazla etkilenecektir.  Başka deyişle, parçacığın konumunu daha kesin ölçmek için uğraştığınızda hızını daha hatalı ö1çüyor olacaksınız, ya da tersine. Heisenberg’in belirsizlik ilkesi dünyanın temel kaçılamaz bir özelliğidir.

 

 

Belirsizlik ilkesi, dünyaya bakış açımıza ta derinden dokunur.  Aradan yetmiş yıldan fazla zaman geçmiş olmasına karşın, etkileri çoğu düşünürce kavranamamış olup hala büyük tartışma konusudur.  ^[5]   İnsanların mutlak bir kesinlikle kabul edebileceği gerçeği doğanın temel parçacıkları düzeyinde bile kendini göstermektedir.  Pozitivizm’in sonu...

 

Yapının Yıkılışı

1900’lü yıllarda Saussure ile başlayarak gelişen ve günümüz düşünce biçimini derinden etkileyen dil bilim çalışmaları ve yapısalcılık kuramı şunu öngörmekteydi... Etrafımızı çevreleyen şeylerin özünde ne olduğuna dair tam ve eksiksiz bir bilgiye ulaşılamayabilir; ancak etrafımızı çevreleyen şeylerin arasındaki ilişkileri inceleyebilirdik.   Bu düşünce insanın “anlamlı biçimde düşünmesini sağlayan şey nedir?” sorusunun sorulmasını gerekli kılmıştır. İnsanın düşünce yapısı belli kavramlara atanmış belli imgelerden oluşumaktadır.  Belli bir düşünce ve kavramlar bütünü bir imgeyle etiketlenmekte ve düşünce yapısı bu etiketler ve etketleri etiketleyen diğer etiketlerle genişleyerek bir yapı oluşturmaktadır.  Bu anlamda etiketler birbirlerinden ayrılabildikleri sürece anlam kazanırlar.  Ses imgelerinden bahsedersek (dildeki en küçük etiketler olarak düşünülebilirler) “a” sesi ile “e” sesi bir birlerinden farklı olduklarından dolayı anlamlı düşünmemizi olanaklı kılan dil yapısını oluşturmak için kullanılabilirler.  İnsan düşüncesindeki kavramlar da benzer farklılıklara göre yapılandırılmıştır.  Her kavram karşıtıyla var olur (iyi / kötü,  aydınlık / karanlık gibi...  ) 

 

Yapı kavramı 20. yüzyılın ortalarında Derrida tarafından getirilen esaslı bir eleştiriyle karşılaşmak zorunda kalmıştır.  Derrida insanların düşünmeyi ses imgeleri ile gerçekleştirdiği önermesinin çok da fazla bir anlamı olmadığını düşünmektedir.  Bu sonsuza kadar giden etiketleme sürecinin ancak tüm etiketlerin üzerinde, aşkın (transandantal, tanrısal) bir etiket olması koşulunda bir anlam taşıyabileceğini söylemektedir. ^[5]    Ona göre tüm düşünce ve duygularımızla ilgili kavramlarımız ve bu kavramları etiketlemek için kullandığımız imgeler arasındaki bağ yapaydır ve koparılmak içindir. Bir kez bu bağ koparıldığında şimdiye kadar düşünmediğimiz şeyleri düşünebilme olanağı elde edilebilir.

 

 İnsanların imgelerle düşünmesi düşüncesi serbest kalınca Baudrillard’ın düşüncelerinin sahne aldığı bir dünya daha iyi anlaşılabilir.  Postmonernitenin en özgün ve etki alanı geniş kurmacılarından biri olarak çalışmalarını ortaya koyuş biçimi gerçeğin temsilinden çok, gerçeğe aşkın bir söylemi bulup çıkarmaktır.  Baudrillard’a göre içinde yaşadığımız toplum,  imajlar ve iletişimle belli bir doymuşluk noktasına ulaşmış bir medya toplumudur.  McLuhan’ın “medya mesajın kendisidir” özdeyişini doğrularcasına simülasyon tarafından domine edilen bir toplumda yaşamakta olduğumuzu düşünmektedir.  Nesneler ve anlatıların artık sağlam bir temele ya da gerçeğe referansta bulunduğunu söylemek güçtür. “Simulacra é Simulasyon” adlı yapıtında  postmodern kültürün  gerçeklikle bağımızı koparan bir göstergeler dünyası olduğu öngörülmektedir. 

 

Matrix: Sayısal Görüş ( http://www.whatisthematrix.com )

 

Baudrillard’ın simülasyonu, gerçeğin gerçekliğe özgün yada onunla bağlantısı olmayan mitolojik veya kavramsal modeller yoluyla yaratılmasıdır.  Model, gerçeklik algısını yöneten konumuna gelir.  Kültür endüstrisi gerçeklerle bilgi (enformason), bilgiyle eğlence, eğlenceyle politika arasındaki çizgiyi silikleştirmektedir.   Kitleler söz konusu imge (simulasyonlar) ve göstergeler (simulacra) tarafından bombalanırken satınalmaya, oy kullanmaya, çalışmaya ve oyun oynamaya karşı cesaretlendirilirler; ancak sonunda fesatlaşırlar.  Bu sosyal düzensizlik durumu anlamın, medyanın ve sosyal yapının çöküşüne yol açar.  Simülasyon ve simülakra gerçek halini alır ve ortada üzerine kuramların, politikanın vs. inşa edilebileceği dengeli bir yapı kalmaz. (Bu noktada Matrix filminden söz etmeden geçersek hayal kırıklıkları gündeme gelebilir.  Filmde, insanları simülasyon uykusundan uyandıracak kahraman Neo’nun, kendini tavşan deliğinin derinlerine götürecek olan beyaz tavşana vereceği illegal yazılımı sakladığı kutu “Simulacra and Simlation”  kitabı görünümündeki bir kutudur ve açtğında görülen bölümün adı “On Nihilism”dir.) ^[7]

 

Mimarinin Doğrusal Olmayan Denklemi

Bilimden sanata ve toplumbilime kadar tamamen oynaklaşmış bir zemine  fırlatılan bu düşünceler, oluşturdukları kimilerince aşırı nihilist bulunan yeni paradigma içerisinde sadece eleştirel olmakla yargılansa da, gerçek dediğimiz olgunun gözden geçirilmesi yolunda yeni perspektifler sunmuşlardır.  Söz konusu “aşırı” eleştirel düşünce ortamında tasarımı artık bir merdivenin rıht yüksekliği ile basamak genişliği arasındaki bağıntıyla ya da işlev ve biçim arasında bir öncelik sıralaması yapmakla açıklamak yetersiz kalmaktadır.   Mimari düşünme ortamı, yapılmak istenen operasyona göre eğilip bükülmektedir.  Binalar artık içinde hangi işlev yer alırsa ona uymak için eğilip bükülmesi gereken kabuklar gibi ele alınmaktadır.  Sadece bir kabuk... Günümüzde bu eğilme, bükülme ya da katlanma (adını siz koyun) bina kabuğuna henüz  uygulanamıyorsa da düşüncelerimize uygulanmasında bir sakınca yok.  Bu dönüştürme düşünce düzeyinde gerçekleşiyor.  Kabukları katlayıp bükebileceğimize, eğip uzatabileceğimize göre tasarım yapıyoruz.  Ya da böyle düşünen tasarımcılara artık “geçeklikle bağlarını koparmış” deliler gözüyle bakılmıyor.  Her ne kadar yaptıklarının mimarlık olmadığını düşünenlerin sayısı az olmasa da...

 

Günümüzün mimarlık alanındaki önemli kuramcılarından (ve uygulayıcılarından) Peter Eisenman’a göre mimarlık bir kararsızlaştırma sürecidir.  One göre mimarlık her şeyin başında, bir şey hakkında düşünce sahibi olmaktır (bu, uzamda ve zamanda herhangi bir şeyi kuramsallaştırmak demektir). İkinci olarak, mimarlık  sadece düşünceyi biçimleştirmek değil ona bir konum vermektir (bu onu eleştirel bir bağlama oturtmak anlamına gelir). Mimarlık bunu hep yapmıştır. Sadece tarihselleştirici değil, aynı zamanda sorunsallaştırıcı bir ajan olmuştur. Mimarlık asla problemleri çözümlemez; onları kendi sert eğilimlerine doğru açar. Tarih yaratan  türden mimarlık hep kuramsallaştırılmış, eleştirel ve sorunsallaştırıcı olmuştur. Brunelleschi Gotiği, ardından Alberti Brunelleschi’yi , Bramante Alberti’yi kararsız bir zemine taşımış ve bu böylece Bromini’ye ve Schinkel’e dek sürüp gitmiştir.

 

Eisenman: Staten İsland İnstitute. Folding Architecture

 

 

Eisenman aynı makalede Jencks’in;

“ Öklidyen olmayan yeni bir uzam kavrayışının var olduğu ve günümüzde Öklidyen duruşun kararsızlaştırlması gerektiği düşüncesini öne sürmüştünüz. Çünkü artık geçmiş değil bugün soz konusuydu.”

yorumuna karşı Öklidyen duruşun, bir zamanlar mimarlığı kararsızlaştırmış olduğunu, bunun kendi zamanında Newtoncu fiziğin ve Darwinci biyolojinin yaptığına denk bir durum ortaya koyduğunu belirtir.  Kendi tasarım yöntemini mimarlık göstergesi ve nesnesi olarak tanımlanan şeye daha az motivasyon içerme olarak ortaya koyar.

“...benim yapmaya çalıştığım,  mimarlık, gösterge ya da nesne zemininde yer alan motivasyon anlamındaki kasıtlılık sorusunu basite indirgemekti. Her koşulda benim çalışmam bu alanlarda ‘daha az motivasyon içerme’ olmuştur.” ^[8]

 

 

Eisenman: Bibliothéque de L’Ihuei. ^[8]

 

Mimarlığa değin bilgiyi oluşturan tüm deneyimler ve bu deneyimlerden çıkan tüm sonuçlar, mimarlıkla ilgili gerçekler kümesinde yer almaktadır.  Mimarlık nesnesi ve göstergesine karşı daha az motivasyon içerme ile anlatılmak istenen, miarlığın gerçeklik kümesinde yer aldığı var sayılan tüm çıkarsamalardan uzaklaşmak olsa gerek.  Mimari operasyonlarımızı gerçekleştirildiğimiz uzayı değiştirmek bir hayal olabilir ama onu eğip bükmek olasılık dışı gibi gözükmüyor.  Bir şeyler tasarlamak adına yola çıktığımızda mevcut durumu ne kadar kararsızlaştırdığımızın önemine katılmamak elden gelmiyor.  Ya da en azından sorgulamak: kararlı bir gerçeklik içinde simulant olarak mı yoksa kararsızlıklarla dolu tavşan deliğinden yuvarlanarak mı bir şeyler aranması gerektiğini...

 

 

Notlar:

[1] Öklidyen Olmayan Geometri ile ilgili tüm bilgiler için yararlanılan kaynakta 3 Boyut Klein Bottle hakkında bilgilere de ulaşmak mümkündür.

Banchoff, T., F., Beyond The Third Dimension: Geometry, Computer Graphics, and Higher Dimensions,  Scientific American Library, 1990, pp. 179 – 194

[2] Phillips Pavyonu için Internet’te yapılacak aramada Poéme Electronique anahtar sözcüğü ile daha fazla sayfaya ulaşılacağı belirtilmelidir.

 

[3] Poéme Electronique’in Edgar Varese’ya ait olduğu söylenen çizimine aşağıdaki linkten ulaşılabilir. Aynı linkte müzikten yapılan küçük bir alıntı bölüm de bulunmaktadır. 

 http://www.geocities.com/vaderv_2000/new/poeme.htm   

Poéme Electronique’in grafik gösterimi aşağıdaki linkten alınmıştır:

 http://www.stanford.edu/~aigeanta/poeme/

(Tarih: 03. Mart. 2003)

 

[4]  The new paradigm and September 11th: Peter Eisenman in conversation with Charles Jencks [interview] / Charles Jencks Architectural design 2002 July, v.72, n.4, p.100

 

[5]  Heisenberg ve Belirsilik kuramı belirtilen eserin ilgili sayfalarından değiştirme yapılmadan alımıştır. 

 Hawking, S., W.; Zamanın Kısa Tarihi, Çeviren: Dr. Sabit Say, Murat Uraz; Milliyet Yayınları, 1989,  s. 79-81,

 

[6]  Derrida’nın Yapıbozum düşüncesinin temelindeki görüş için:

Derridai J., Of Grammatology, The Johns Hopkins University Press, 1997, p. 20

 

[7] Baudrillard’ın Simulacra &  Simulation yapıtı hakkındaki bilgiler için aşağıdaki internet sayfasından yararlanılmıştır.  Tarih: 03.Mart. 2003  http://www.uta.edu/english/hawk/semiotics/baud.htm

 

[8]Eisenman ve Jencks’ten alıntılar: The new paradigm and September 11th: Peter Eisenman in conversation with Charles Jencks adlı makaleden. pp. 99

                                 

[9] Eisenman’ın Staten İsland İnstitute ve Bibliothéque de L’Ihuei çizimleri

Eisanman, P., Dagram Diaries, Universe Publishing, 1999, pp. 159, 208